垂心 の 位置 ベクトル
センス の いい プレゼント 女性 10000 円【高校数学b】三角形の垂心の位置ベクトル | 受験の月. 垂心の位置ベクトル{垂心は, 3頂点から対辺に下ろした垂線の交点である. まず, 先を見越して内積の値を求めておく. 先を見越せなければ, 必要になった時点で求めればよい. 垂心 の 位置 ベクトル【垂心とは?】三角形の五心と位置ベクトルを解説!垂心の . 三角形ABCの垂心をH、外心をOとすると、それぞれの位置ベクトルは以下のように表すことができます。 これには以下のような三角形と位置ベクトルの性質が関係しています。. 垂心 - ベクトル Oh |位置ベクトルで表示する【図形の証明も . 垂心については、各頂点から向かい合う辺に下した三本の垂線が、1点のみで交わることの証明を平面図形の単元で学習します。. この図形的な内容に、さらにベクトルの内容を加えて、垂心の位置ベクトル表示が得られます。. まずは、三本の垂線が . 垂心 の 位置 ベクトル外心と垂心の位置ベクトル - 高校数学.net. 外心と垂心の位置ベクトル. ABC の外心 O 、垂心 H. 外心の位置ベクトルの求め方. 垂心 の 位置 ベクトル→ AO = s→ AB + t→ AC. 頭皮 の 皮脂 が 多い
頭痛 に 効く サプリ{ → OM ⋅ → AB = 0 → ON ⋅ → AC = 0. 垂心の位置ベクトルの求め方. → AH = s→ AB + t→ AC. { → CH ⋅ → AB = 0 → BH ⋅ → AC = 0. 三角形の五心を忘れている . 位置ベクトルの定義と基本例題の解説 | 高校数学の美しい物語. みなと 住 建 評判
て じ 韓 小牧垂心の位置ベクトル. 位置ベクトルの定義・意味. 垂心 の 位置 ベクトル髪 を 触る と 頭皮 が 痛い
ビール を 地面 に 撒く 会まず, ベクトル とは,向きと大きさを持つ量のことです。 矢印(向きのある線分)と考えてもよいです。 そして, 位置ベクトル とは「点の位置を表すベクトル」です。 もう少し正確な定義は以下です: 位置ベクトルの定義. 前提として,基準となる点 O O がある。 このとき,ベクトル overrightarrow {OP} OP のことを点 P P に対する 位置ベクトル と呼ぶ。 基準となる点 O O のことを原点と呼びます。 原点 O O があるとき,「 O O を始点とするベクトル」と「点」は1対1に対応します。 つまり, どこかに点. P P をうつとベクトル. overrightarrow {OP} OP が決まる. 逆に,. 垂心 の 位置 ベクトル垂心・内心・外心の位置ベクトルと証明問題 | Hatsudy:総合 . 垂心とは、三角形の頂点から辺に対して垂直に引いた線の交点を指します。 そのため OABについて、頂点から垂心Hに引く線と三角形の辺は必ず直角になります。 OH ⊥ AB. AH ⊥ OB. 垂心 の 位置 ベクトルBH ⊥ OA. 直角というのは、ベクトルの内積がゼロになることを意味します。 また、もう一つ利用するべき性質があります。 一つのベクトルを二つのベクトルに分解することができるのです。 そこで、 OH−→− を以下のように分解しましょう。 OH−→− = s a→ + t b→. s や t の値は不明です。 ただ同じ平面上に存在するため、このようにベクトルを分解することが可能です。 垂心の位置ベクトルでは、この性質を利用することで問題を解きましょう。 それでは、以下の問題の答えは何でしょうか。. PDF 三角形の垂心の位置ベクトル - gleamath.com. 注意. 垂心 の 位置 ベクトル垂心の定義から,A = 90 である直角三角形ABCにおける垂心は,頂点Aに一致する. 1三角形の各頂点から,その対辺または延長線に下ろした垂線の交点を垂心という. 2加重重心の拡張leamath.com/weighted-center02/. 【2021京都大学・文】垂心の位置ベクトル|頻出・基本問題 . 垂心とは,三角形の各頂点から対辺におろした垂線の交点. 垂心 の 位置 ベクトル考え方. ① 点 H は OAB 上より共面条件. 垂心 の 位置 ベクトル👉 実数 s , t を用いて. OH−→− = sOA−→− + tOB−→− とおける. ※ 共面条件についての詳細・例題は「 ② 点 H は垂心. 👉 OH ⊥ AB かつ AH ⊥ OB. 垂心 の 位置 ベクトル⇒ OH−→− ⋅ AB−→− = 0 かつ AH−→− ⋅ OB−→− = 0. 解答. 0AB において, OA = 3 , OB = 2 , ∠AOB = 60° とする. OAB の垂心 H とするとき, OH−→− を OA−→− と OB−→− を用いて表せ.. 実数 s , t を用いて. OH−→− = sOA−→− + tOB−→− とおける. 三角形の垂心について知っておきたい知識まとめ | 理系ラボ. 2. 三角形の垂心の定理の証明. 「三角形の3つの各頂点から対辺(またはその延長)に下ろした垂線は1点で交わる」ことを証明していきます。 ( mathrm{ triangle ABC } )の頂点( mathrm{ A, B, C } )から対辺(またはその延長)に下ろした垂線を、それぞれ( mathrm{ AD, BE, CF } )とします。 また、( mathrm{ A, B, C } )の各頂点を通り、それぞれの対辺に平行な直線の交点を、( mathrm{ P, Q, R } )とします。. 垂心 の 位置 ベクトル三角形の垂心の位置ベクトル - gleamath.com. 高校数学 By gleamath. 三角形があれば,その 垂心 が存在する.. よって,三角形の 3 頂点の位置ベクトルを用いて, 垂心の位置ベクトルを表すことができる.. 本稿では, 加重重心の結果 を用いて, 垂心の位置ベクトルの美しい表示を与える.. 垂心 の 位置 ベクトル命題. 3 点 A(a ),B(b ),C(c ) を頂点とする ABC の垂心を H(h ) とする.. このとき, h = (tanA)a + (tanB)b + (tanC)c tanA + tanB + tanC. が成り立つ.. ただし, ABC は直角三角形ではないとする.. PDF. ベクトル. 三角形の垂心とは?垂心の性質と証明. 垂心 の 位置 ベクトル垂心の位置ベクトル 三角形ABCの垂心をHとすると、垂心の位置ベクトルは以下のように表すことができます。[displaystyle vec{h} =frac{tan A vec{a} + tan B vec{b} +tan C vec{c}}{tan A +tan B +tan C}] これには以下のような三角. 五心とは?三角形の重心/内心/外心/垂心/傍心の性質と求め方 . 三角形の垂心の位置も、内心・外心と同様に各頂点の位置ベクトルを用いて表すことができます。 垂心の位置ベクトルの公式 (triangle mathrm{ABC}) の各頂点の位置ベクトルを (mathrm{A}(vec{a})), (mathrm{B}(vec{b})), (mathrm{C}(vec{c})) とする。. 【高校数学a】三角形の重心・外心・垂心の位置関係(オイラー線 . 2020.11.23. ベクトルを用いた証明はこちら。 ベクトルとオイラー線(三角形の重心G・外心O・垂心Hの位置関係) 定期試験・大学入試対策に特化した解説。 ベクトルを用いるとOG:GH=1:2であることの証明が容易にできる。 GeoGebra動画。 examist.jp. 3頂点A,B,Cを動かして直角三角形や直角二等辺三角形や鈍角三角形を作ってみましょう。 正三角形では重心・外心・垂心が一致するためにオイラー線は存在しないので描かれません。 しかし、手動で完全な正三角形を作ることはできないので正三角形にするボタンを作成しています。 検索用コード. 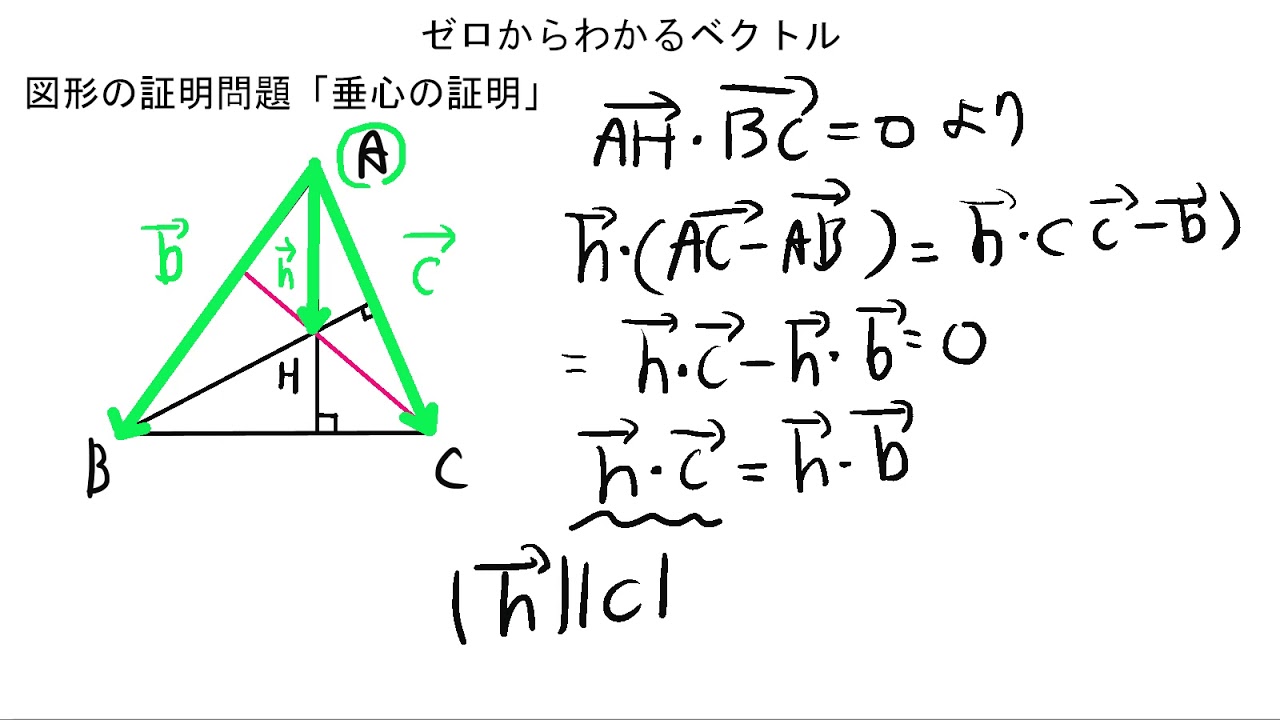
癌 頭 に 転移三角形の五心の覚えておくべき性質を整理 | 高校数学の美しい物語. 内心の位置ベクトル i undefined overrightarrow{i} i は各頂点の位置ベクトルを用いて以下のように表される: i undefined = a a undefined + b b undefined + c c undefined a + b + c overrightarrow{i}=dfrac{aoverrightarrow{a}+b i = a + b +. 垂心 の 位置 ベクトル位置ベクトルを超わかりやすく解説した(内分・外分・重心 . 位置ベクトルとは? 平面上で1点 ( O ) を固定して考えると,任意の点 ( P ) の位置は,ベクトル ( vec{ p } = overrightarrow{ OP } ) となります。 このとき. 「( vec{ p } ) は点 ( O ) に関する点 ( P ) の位置ベクトル」 といい,( color{red}{ P ( vec{ p } ) } ) と表します。 補足. 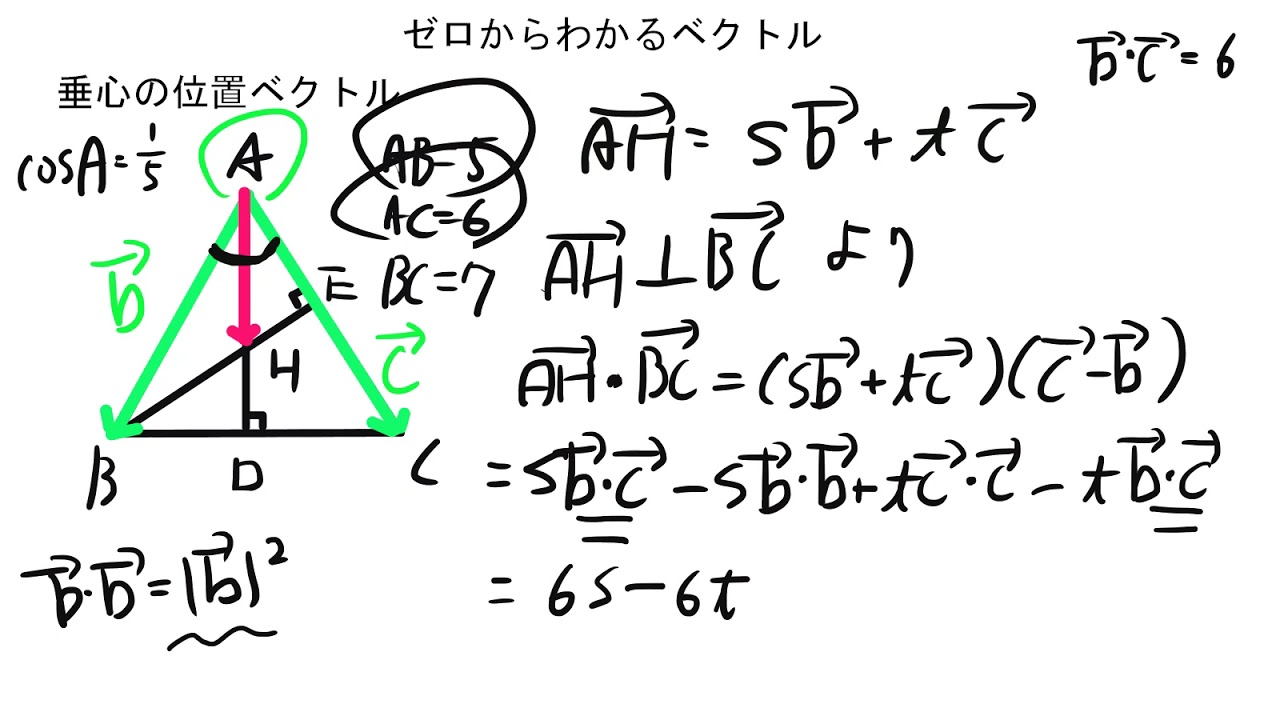

お金 に 苦労 する スピリチュアルで, , , の二等分線と辺 , , の交点をそれぞれ , , とすると, 直線 , , は 点 で交わる。 この点 が c. の 内心 である。 図 で「 b . 垂心の位置ベクトル - YouTube. 垂心 の 位置 ベクトル垂心の位置ベクトル. はやくち解説高校数学. 垂心 の 位置 ベクトル18.9K subscribers. Subscribed. 231. 11K views 6 years ago 平面ベクトル 典型18題. <問題> OA=2√2,OB=√3,ベクトルOAとベクトルOBの内積が2である三角形OABの垂心Hに対して,ベクトルOHをベクトルOAとベクトルOBを用いて表せ. .more. .more. ベクトルとオイラー線(三角形の重心G・外心O・垂心Hの位置関係). Geogebra動画。 examist.jp. 垂心 の 位置 ベクトル3頂点A,B,Cを動かして直角三角形や直角二等辺三角形や鈍角三角形を作ってみましょう。 正三角形では重心・外心・垂心が一致するためにオイラー線は存在しないので描かれません。 しかし、手動で完全な正三角形を作ることはできないので正三角形にするボタンを作成しています。 検索用コード. 垂心 の 位置 ベクトルABCにおいて, 重心をG, 外心をOとする. $OH}=OA}+OB}+OC} を満たす点 {H}は垂心であることを示せ.$ 3点O, G, Hが一直線上にあり, $ {OG:GH=1:2}$であることを示せ. 内心 - ベクトル | 三角形に内接する円の中心を表示する【平面 . 1. 内心 :内部で交わる1点. 1.1. 角の二等分線と辺の交点と内分比. 1.2. 比の値をよく見る. 2. 内心 : 位置ベクトルで表示する. 2.1. 同様の議論をもう一度. 垂心 の 位置 ベクトル2.2. 垂心 の 位置 ベクトル位置ベクトル表示を完了. 垂心 の 位置 ベクトル2.3. 垂心 の 位置 ベクトル三角形の五心について. 内心 :内部で交わる1点. 三角形ABC が与えられたとします。 BC = p, CA = q, AB = r という辺の長さとします。 そして、∠A, ∠B, ∠C の二等分線が、それぞれの対辺と交わる点を D, E, F とします。 次の図のような状況になっています。 ここで、直線AD と直線BE は平行でないため、1点 X で交わります。 しかし、直線CF も点 X で他の二本の角の二等分線と交わるかどうかは、これだけでは不明です。. ベクトルと三角関数で表した内心,外心,重心,垂心. 外心,重心,垂心は1直線上にあることを示すことができる.(内心は,これら3点と同一直線上にあるとは限らない). 垂心 の 位置 ベクトル(5.1)を直接示そうとすると, の 差 を比較することになるが,これらはすでに複雑な三角関数の分数式になっているので,通分などが容易 . 外心・重心・垂心とオイラー線 - 高校数学.net. 三角形の外心と重心と垂心とオイラー線. 垂心 の 位置 ベクトル三角形の外心と重心と垂心は三角形が正三角形はじゃないとき一本の直線上にあるんだ。 この直線のことを オイラー線 っていうんだ。 今回はこのオイラー線を外心を始点にしたベクトルで考えてみよう。. 外心とは?三角形の外心の座標・位置ベクトルの求め方や性質の証明をわかりやすく解説!【垂心】 | 遊ぶ数学. 垂心 の 位置 ベクトルこんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の外心(+垂心)」 について、性質の証明や座標の求め方、位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心とは なぜ"外心"なのか、いきなり説明することは. 三角形の五心(垂心)〜位置ベクトルの一般化〜 - YouTube. 福岡で数学塾をしています!キャッチフレーズは「学年を超える数学」中高生から大人まで大歓迎です♪♪♪【Rmath塾 Twitter】⇒ witter.com . 垂心 の 位置 ベクトル重心 - ベクトル | 三角形の重心を位置ベクトルで表示する【証明】 | 岩井の数学ブログ. 重心 - ベクトル :座標. g → = ( a → + b → + c → )/3 という公式から、重心を表す座標についての公式が導かれます。. 垂心 の 位置 ベクトル重心の位置ベクトル表示ですが、上で導いた議論は、平面ベクトルと空間ベクトルのどちらについても全く同じ議論となります。. そのため . 外心 - ベクトル | 面積比から辺の分点の比を求めるところから | 岩井の数学ブログ. ・ 重心の位置ベクトル ・ 内心の位置ベクトル ・ 垂心の位置ベクトル ・ 傍接円の位置ベクトル. これらについても、ベクトルで表すことを解説しています。 オイラー線 という記事では、外心に関連した図形の内容を解説しています。. オイラー線の3通りの証明 | 高校数学の美しい物語. 美しい定理です。. この直線をオイラー線といいます。. オイラー線の存在を3通りの方法で証明します。. 方法1:初等幾何を用いた証明. 垂心 の 位置 ベクトル方法2:ベクトルを用いた証明. 方法3:三角関数のゴリ押し計算で証明. 証明の途中で,外心・重心・垂心の性質は既知と . 垂心の位置ベクトル | 大学受験の王道. 藤ヶ谷 亮輔
米 を 研ぐ ザル垂心の位置ベクトル. 2021年1月26日 kyogaku-juku. (1)問題概要. 垂心(三角形の各頂点から対辺に下した垂線の交点)の位置ベクトルを求める問題。. (2)ポイント. 垂心 の 位置 ベクトルまずは、三角形OABの垂心をHとおき、. ① OHベクトル=s (aベクトル)+t (bベクトル) とし、そして . ベクトルと三角関数で表した内心,外心,重心,垂心. 外心,重心,垂心は1直線上にあることを示すことができる.(内心は,これら3点と同一直線上にあるとは限らない). (5.1)を直接示そうとすると, の 差 を比較することになるが,これらはすでに複雑な三角関数の分数式になっているので,通分などが容易 . 重心とは?三角形の重心の座標・位置ベクトルの求め方や公式の証明・面積比の問題を解説!【数学】【オイラー線】 | 遊ぶ数学. 垂心 の 位置 ベクトルこんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の重心」 の座標・位置ベクトルの求め方や、その公式の証明、また重心の重要な性質を利用した面積比を求める問題などをわかりやすく解説していきます。 また、記事の後半では、三角形. 垂心の位置ベクトル(ゼロからわかるベクトル第23回) - YouTube. 苦手な方向けのベクトルの授業です。今回は前回の授業で触れた方法を使って垂心の位置ベクトルを基準ベクトルの和に変換する問題を取り上げ . 【高校数学b】三角形の内心の位置ベクトル | 受験の月. 三角形の内心の位置ベクトル. ABCにおいて, AB=5, BC=7, CA=6 とする.}$ を用いて表せ.}$ 内心の位置ベクトル 内心 (内接円の中心)は, 三角形の3つの内角の二等分線の交点である. 垂心 の 位置 ベクトル内心の位置は, 角の二等分線と辺の比の関係 (数A:平面図形)を2回適用して求め . 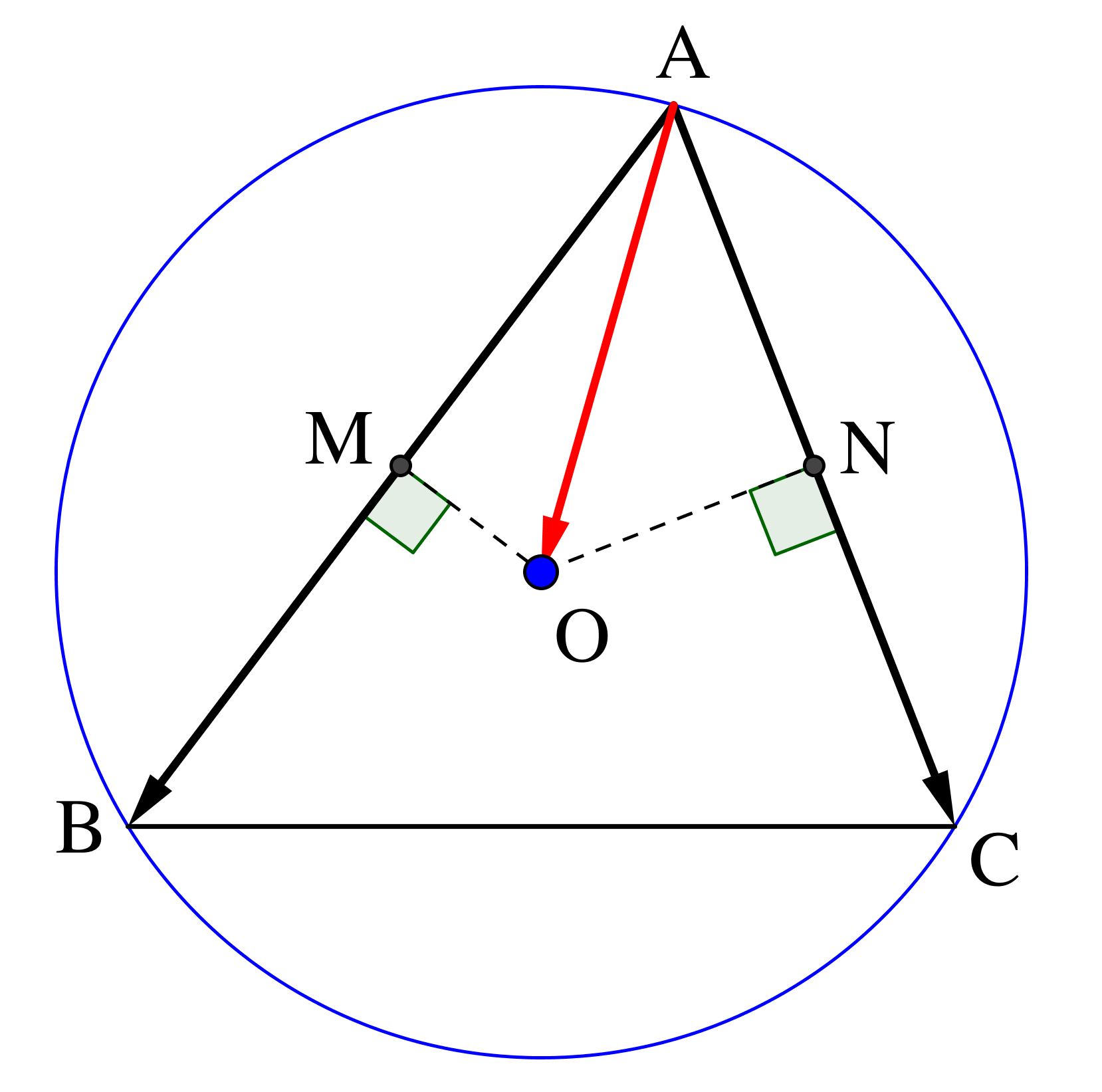
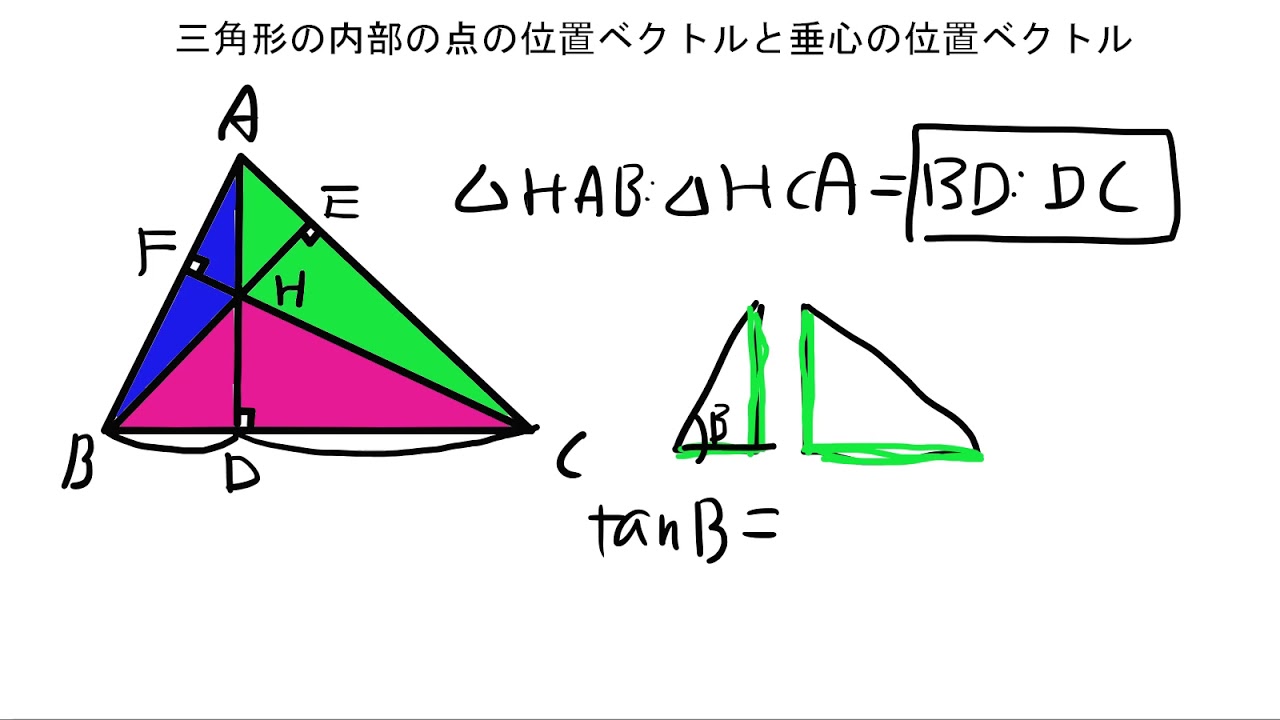
部屋 の 温度 を 上げる 熱量中線とは、頂点と、対辺の中点とを結ん . 勉強しよう数学解答集: 三角形の垂心の位置ベクトルの計算. すなわち、ここでは、「(2)ベクトルmとcが垂直である条件として 内積が0であるというベクトル方程式 を作る」ことをしないで、別のベクトル方程式を作って問題を解いてみます。 【問0】三角形の垂心Oの位置ベクトルをもとめよ。. PDF series 高校数学こぼれ話 第 数学科部長 渡邉泰治. 三角形の外心 O、重心 G、垂心 H の間に「O, G, H は同一直線上にあり、2 OG=GH 」 という関係がある(図 3 上)。この直線は発見者オイラー(Euler, 1707-1783年)因んで オイラー線と呼ばれている。この証明はベクトルを使うと簡便であり、概要は次のとおり. 垂心 の 位置 ベクトル外心と垂心. abc の外心 e の位置ベクトルを求めてみよう。 ここで数学の一般常識として, abc に於いて, ∠a の大きさを唯単に a, 同様に ∠b を b, ∠c を c と, 又, 辺 bc の長さを (対角の記号を用いて) a, 辺 ca を b, 辺 ab を c と略記することに注意しておく。. 【高校数学b】円のベクトル方程式2パターン | 受験の月. 垂心 の 位置 ベクトル2直線の交点の位置ベクトル(ベクトル分野ダントツNo.1頻出問題) 加重重心(裏技)による点Pの位置問題と交点の位置ベクトル問題; 角の二等分線のベクトル2パターン; 正射影ベクトル(直交射影ベクトル) 三角形の内心の位置ベクトル; 三角形の垂心の位置 . 傍心 | 傍接円の中心を位置ベクトルで表示する | 岩井の数学ブログ. ipo チャレンジ ポイント 急 に 増え た
フォロー しない で フォロワー を 増やす twitterHatena. アシュワース とは
試験 前日 寝れ ないLINE. Copy. " 傍接円 "の中心である傍心は、三角形の一つの頂点と内心を通る直線と、外角の二等分線の交点になっています。. この内容を位置ベクトルを用いて表すことで、傍心をベクトルで表せます。. 平面図形で学習した内容を、ベクトルを用いて . 位置ベクトルとは?内分点・外分点・三角形の重心の求め方を解説!【応用問題の解き方】 | 遊ぶ数学. こんにちは、ウチダです。 今日は数学bのベクトルで習う 「位置ベクトル」 について、まず位置ベクトルとは何なのか、次に位置ベクトルとベクトルの違い、そしていろんな位置ベクトルの求め方とその応用について解説していきます。 また後半では、位置ベ. 平面ベクトルの基本 - 高校数学.net. ベクトルの平行移動と実数倍. 垂心 の 位置 ベクトルベクトルは向きと大きさをもつものだけど、 平行移動しても同じベクトルと見なすことができる 。 つまり ベクトルは位置によらず、どこにあっても向きと大きさが一緒なら等しいベクトル ってことになるんだ。. 勉強しよう数学: 三角形の垂心の位置ベクトルの公式を初めて学ぶ方法. その円上の3点A,B,Cが作る三角形の垂心の位置ベクトルHを求めよ。 この問題の解答はここをクリックした先にあります。(パラドックスの話もあります)。 (参考問題)「外心を原点にした場合の垂心の位置ベクトル」 リンク: 高校数学の目次. 数Cベクトルと平面図形④垂心の位置ベクトル - YouTube. 【動画目次】00:00 op01:14 垂心の性質02:17 練習問題1動画ご視聴ありがとうございました。本チャンネルでは、高校数学の解説を行っております。. 拡声 器 どこで 売っ てる